二叉树
介绍
每个结点最多有两个子节点,有左右之分。
它具有以下特点:
- 在二叉树的第i(根结点为1层)层上最多有2^(i-1)个结点(i>=1)
- 高度为k的二叉树,最多有2^k-1个结点(k>=0)
- 对任何一棵二叉树,如果其叶结点有n个,度为2的非叶子结点有m个,则 n=m+1
分类
- 满二叉树:除最后一层无任何子节点外,每一层上的所有结点都有两个子结点的二叉树。
- 完全二叉树:叶子结点只存在在最后一层或倒数第二层。并且如果最下面一层节点不满,则所有的节点在左边的连续排列,空位都在右边。
- 平衡树:它是一 棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。平衡树有很多常用的使用方法,比如有红黑树、AVL等。
- AVL:加了平衡条件的二叉搜索树,因为平衡后深度更浅,那么搜索的性能更高了。
| 分类 | 说明 | 图示 | 备注 |
|---|---|---|---|
| 满二叉树 | 所有分支都有左子树和右子树,且所有叶子节点在同一层。 | 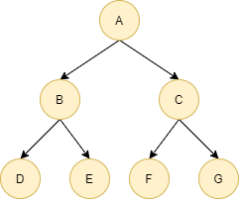 |
|
| 完全二叉树 | 对二叉树按照从上到下、从左到右编号。
如果二叉树节点编号,与满二叉树对应节点编号相同。
|
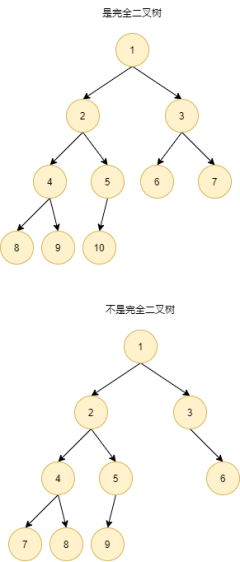 |
|
| 斜树 | 所有的结点都只有左子树(左斜树)
或者只有右子树(右斜树)。 斜树应用场景较少。 |
无|缩略图 | |
| 二叉排序树 | 二叉排序树,又称二叉查找树,也叫二叉搜索树。
特点:
|
无|缩略图 | |
| 平衡二叉树 | 平衡二叉树(Balanced BinaryTree)又被称为AVL树(有别于AVL算法)
它是一棵空树或它的左右两个子树的高度差的绝对值不超过1 并且左右两个子树都是一棵平衡二叉树。
|
无|缩略图 |
遍历
四种遍历方式
| 深度优先
(DFS) |
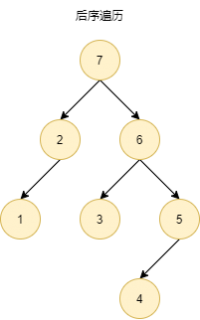
前序遍历 | 中序遍历 | 后序遍历 |
|---|---|---|---|
| preorder traversal | inorder traversal | postorder traversal | |
| 根→左→右 | 左→根→右 | 左→右→根 | |
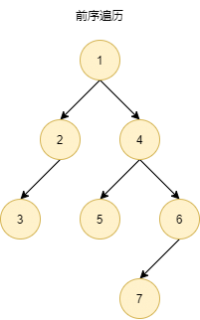 |
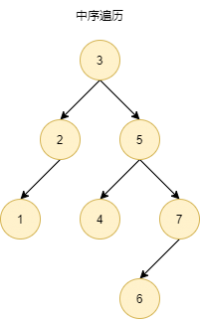 |
 | |
| 广度优先
(BFS) |
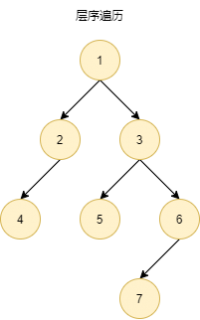
层序遍历 | ||
| levelorder traversal | |||
 |
记忆方式
左右根记忆:前中后指的是根的位置,然后剩下两个位置按照左右顺序补充:
- 前序遍历:根在前,根→左→右
- 中序遍历:根在中,左→根→右
- 后续遍历:根在后,左→右→根
确定遍历方式之后,如何推导出节点遍历顺序?
不靠死记硬背,用推导的方式。
从根节点开始:
- 如果是中节点,打印值
- 如果是左右节点,看它是否是一颗子树
- 如果是,进行递归
- 如果不是,打印值
编码实现
递归法:
- 先写截止条件
- 之后按照顺序
- 如果是根,就直接打印
- 如果是左右,则递归调用即可
非递归法:
要把递归写法改成迭代写法,需要用到的一个很重要的数据结构:栈,用它来保存我们上一个结点,也就是记录我们从哪里来,这样在处理完某个结点的时候,我们可以通过栈来倒退回上一步,这就是迭代写法的核心。
我发现有两种实现方法,还有一种单重循环就能实现的。 根→左→右
LeetCode 144题
| 类别 | 实现方式 | 具体代码 | 关联题目 |
|---|---|---|---|
| 前序遍历 | 递归实现 | public class PreOrderTree {
// 递归先序遍历
public void preOrderRe(Node node){
if (node == null) return;
System.out.println(node.value);
preOrderRe(node.left);
preOrderRe(node.right);
}
}
|
|
| 非递归实现 | public class PreOrderTree {
// 非递归先序遍历
public void preOrder(Node node){
Stack<Node> stack = new Stack<>();
while (!stack.isEmpty()||node!=null){
while(node!=null){
System.out.println(node.value);
stack.push(node);
node=node.left;
}
node=stack.pop();
node=node.right;
}
}
}
| ||
| 中序遍历 | 递归实现 | public class MidOrderTree {
// 中序递归遍历
public void midOrderRe(Node node){
if (node==null){
return;
}else{
midOrderRe(node.left);
System.out.println(node.value);
midOrderRe(node.right);
}
}
}
|
|
| 非递归实现 | public class MidOrderTree {
// 中序非递归遍历
public void midOrder(Node node){
Stack<Node> stack = new Stack<>();
while(!stack.isEmpty()||node!=null){
while(node!=null){
stack.push(node);
node=node.left;
}
node = stack.pop();
System.out.println(node.value);
node = node.right;
}
}
}
| ||
| 后序遍历 | 递归实现 | class Solution {
List<Integer> res = new ArrayList<>();
public List<Integer> postorderTraversal(TreeNode root) {
if(root == null) return res;
dfs(root);
return res;
}
public void dfs(TreeNode root){
if(root == null) return ;
dfs(root.left); //遍历左子树
dfs(root.right); //遍历右子树
res.add(root.val); //遍历根节点
}
}
|
|
| 非递归实现 | class Solution {
public List<Integer> postorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<>();
Stack<TreeNode> stk = new Stack<>();
if(root == null) return res;
while(root != null ||!stk.isEmpty()){
while(root != null){
res.add(root.val); //遍历根节点
stk.push(root); //记录遍历路径
root = root.right; //遍历右子树
}
root = stk.pop(); //出循环时root为null,回到上一步(即栈顶)
root = root.left; //遍历左子树
}
Collections.reverse(res); //反转结果
return res;
}
}
|
归档:
中序遍历
中序遍历的关键在于:先遍历左子树,再遍历根节点,最后遍历右子树。
即:左→根→右。
非递归
同样的道理用栈来记录我们的遍历路径,代码与前序遍历十分相似。
递归
后序遍历
后序遍历的关键在于:先遍历左子树,再遍历右子树,最后遍历根节点。
即:左→右→根。
非递归
后序遍历的迭代写法稍微有一点不同,需要转换一下思路,如果我们直接去写的话会发现并不好写,所以我们可以观察一下特点:
前序遍历的顺序是:根左右,后序遍历的顺序是:左右根,如果把前序遍历的结果反转一下就是:右左根,和后序遍历的顺序差在左右子树的遍历顺序上,所以后序遍历的迭代写法可以在前序遍历的迭代写法上进行小小的修改。
即:先遍历根节点,再遍历右子树,最后遍历左子树。得到的结果最后反转一下,就是二叉树的后序遍历。
递归
层序遍历
public class tree {
//非递归层序遍历
public static void levelOrder(Node root){
Node p=root;
Queue<Node> queue= new LinkedList<>();
queue.offer(p);
while(!queue.isEmpty()){
p = queue.poll();
System.out.print(p.value+" ");
if(p.left!=null){
queue.offer(p.left);
}
if(p.right!=null){
queue.offer(p.right);
}
}
}
}
二叉树深度
public class tree {
//求输的最大深度
static int depth(Node node){
if(node==null){
return 0;
}
int m=depth(node.left);
int n=depth(node.right);
return Math.min(m,n) + 1;
}
}
两个二叉树是否相等
public static boolean isEqual(Node node1,Node node2){
if (node1 == null && node2 == null) {
return true;
}
if ((node1 == null && node2 != null)) {
return false;
}
if ((node1 != null && node2 == null)) {
return false;
}
if (!node1.value.equals(node2.value)) {
return false;
}
return isEqual(node1.left, node2.left) && isEqual(node1.right, node2.right);
}
统计二叉树的叶子结点个数
public static boolean isEqual(Node node1,Node node2){
if (node1 == null && node2 == null) {
return true;
}
if ((node1 == null && node2 != null)) {
return false;
}
if ((node1 != null && node2 == null)) {
return false;
}
if (!node1.value.equals(node2.value)) {
return false;
}
return isEqual(node1.left, node2.left) && isEqual(node1.right, node2.right);
}
存储
在计算机中,存储方式只有两种,一个是数组,一个是链表。
数组是存储在连续的内存上,所以我们可以根据偏移量直接找到内存的地址,但是在我们插入和删除元素时,因为要保证连续性,需要把前移或后移保证连续性,效率比较低。
链表,相当与一个链条,不需要存储在连续的内存上,只要第一个结点保存下一个的引用即可,这样我们随机访问就不能通过内存的偏移量直接找到地址了,而需要从第一个位置往后遍历,随机访问效率比较低,但是插入和删除的效率比较高,因为我们不用移动元素,只要修改下一个结点的引用既可。
树型结构也可以通过数组和链表存储。
网络资源
二叉树 :超级肥的兔子
LeetCode 二叉树专题 (1)二叉树知识 和 解题框架 :ZSAchg